AVL Tree란?
AVL 트리란 자가 균형 이진 탐색 트리(Self-Balanced Binary Search Tree)의 한 유형입니다. Adelson-Velsky와 Landis가 1962년에 발명하였으며, 이들의 앞글자를 따서 이름을 붙였습니다. AVL 트리는 각 노드의 서브트리 높이 차이가 최대 1을 유지하도록 스스로 균형을 유지하는 트리인데, 이 서브트리의 높이 차이를 균형 계수(Balance Factor, BF)라 합니다. 그렇기에 삽입과 삭제 연산을 수행할 때마다 트리의 균형 계수를 체크하고, 균형 계수가 1보다 커질 때 회전(Rotation) 연산을 통해 균형을 유지합니다.
Binary Search Tree는 불균형할 때 탐색 성능이 O(logn)에서 O(n)으로 떨어지는 문제가 있었는데, AVL tree는 위같은 방식으로 균형을 유지하여 tree의 성능을 안정적으로 보장할 수 있게 되었습니다.
AVL 트리의 회전 연산은 왼쪽-왼쪽, 오른쪽-오른쪽, 왼쪽-오른쪽, 오른쪽-왼쪽의 네 가지 경우가 있습니다.
AVL 트리는 회전 연산을 통해 균형을 항상 유지하는 Self-Balanced Tree이므로 검색, 삽입, 삭제의 시간 복잡도는 모두 O(log n)으로 보장됩니다. 하지만 AVL 트리는 삽입과 삭제가 일어날 때마다 회전 연산을 수행해야 하기 때문에, 이로 인해 연산 속도가 느릴 수 있습니다. 하지만 회전 연산은 상수 시간(O(1))으로 실행되므로 데이터가 많을수록 이진 탐색 트리보다 평균적인 시간복잡도가 줄어들어 성능이 더 좋습니다. 물론 삽입이 매우 빈번하게 발생하는 경우 AVL 트리보다 회전 연산이 덜 필요한 B- 트리나 R-B 트리가 더 나은 성능을 보일 수 있지만 구현이 복잡하고 메모리 사용량이 크다는 각각의 장단점이 있습니다.
이 글에서는 AVL 트리의 특징, 삽입과 삭제 및 회전 연산, 활용에 대해 설명하겠습니다.
AVL Tree의 특징
AVL 트리의 특징은 다음과 같습니다.
1. 이진 검색 트리(Binary Search Tree)입니다. 이는 각 노드의 왼쪽 하위 트리에는 노드 값보다 작은 값을 가진 노드만, 오른쪽 하위 트리에는 노드 값보다 큰 값을 가진 노드만 포함됩니다.
2. 모든 노드의 두 하위 트리의 높이는 최대 1까지 차이가 납니다.
3. 트리의 모든 노드는 노드에서 리프 노드까지의 가장 긴 경로 길이인 높이 값을 갖습니다.
4. 루트 노드는 높이 0에 위치합니다.
5. 노드의 균형 계수는 왼쪽과 오른쪽 하위 트리의 높이 차이로 정의됩니다. AVL 트리에서 노드의 균형 계수는 항상 -1, 0, 1입니다.
AVL tree의 연산
그렇기에, 새로운 노드가 AVL 트리에 삽입되면 트리가 불균형 상태가 될 수 있습니다. 이때 트리의 균형을 유지하기 위해 이련의 회전 연산(rotation)을 수행하게 됩니다. 회전 연산은 다음과 같은 네 가지 경우가 있습니다.
1. 왼쪽-왼쪽: 노드의 왼쪽 하위 트리에 새 노드가 삽입되어 노드의 균형 계수가 -2가 됩니다.
2. 왼쪽-오른쪽: 노드의 왼쪽 자식의 오른쪽 하위 트리에 새 노드가 삽입되어 노드의 균형 계수가 -2가 됩니다.
3. 오른쪽-왼쪽: 노드의 오른쪽 자식의 왼쪽 하위 트리에 새 노드가 삽입되어 노드의 균형 계수가 2가 됩니다.
4. 오른쪽-오른쪽: 노드의 오른쪽 자식의 오른쪽 하위 트리에 새 노드가 삽입되어 노드의 균형 계수가 2가 됩니다.
각 경우에 따라서 다른 회전을 수행해야 합니다. 왼쪽-왼쪽과 오른쪽-오른쪽의 경우에는 single rotation을 수행하면 됩니다. 왼쪽-오른쪽과 오른쪽-왼쪽의 경우에는 double rotation을 수행해야 합니다.
Single rotation은 노드의 자식 노드를 한 번 회전시켜서 트리의 균형을 맞춥니다. 노드의 왼쪽 하위 트리에 새 노드가 삽입되어 균형이 깨졌을 때는, 노드의 오른쪽 자식 노드를 왼쪽으로 한 번 회전시킵니다. 노드의 오른쪽 하위 트리에 새 노드가 삽입되어 균형이 깨졌을 때는, 노드의 왼쪽 자식 노드를 오른쪽으로 한 번 회전시킵니다. 아래는 왼쪽 하위 트리에 노드가 삽입되었을 때의 예시입니다.
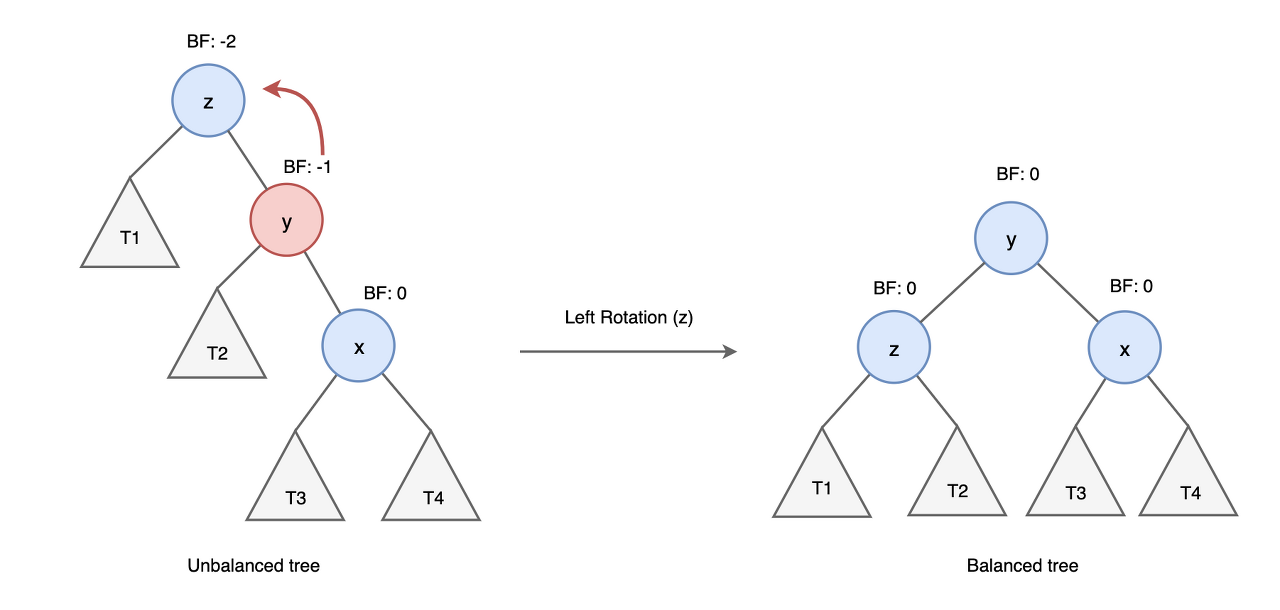
Double rotation은 노드의 자식 노드를 두 번 회전시켜서 트리의 균형을 맞춥니다. 노드의 왼쪽 자식의 오른쪽 하위 트리에 새 노드가 삽입되어 균형이 깨졌을 때는, 노드의 왼쪽 자식 노드를 왼쪽으로 한 번 회전시키고, 그 다음에 노드 자신을 오른쪽으로 한 번 회전시킵니다. 노드의 오른쪽 자식의 왼쪽 하위 트리에 새 노드가 삽입되어 균형이 깨지면 마찬가지로 노드의 오른쪽 자식 노드를 오른쪽으로 한 번 회전시키고, 그 다음에 노드 자신을 왼쪽으로 한 번 회전시킵니다. 이러한 방식으로 AVL 트리의 균형을 유지합니다.
아래는 노드의 왼쪽 자식의 오른쪽 하위 트리에 노드가 삽입되었을때의 왼쪽-오른쪽 rotation 예시입니다.
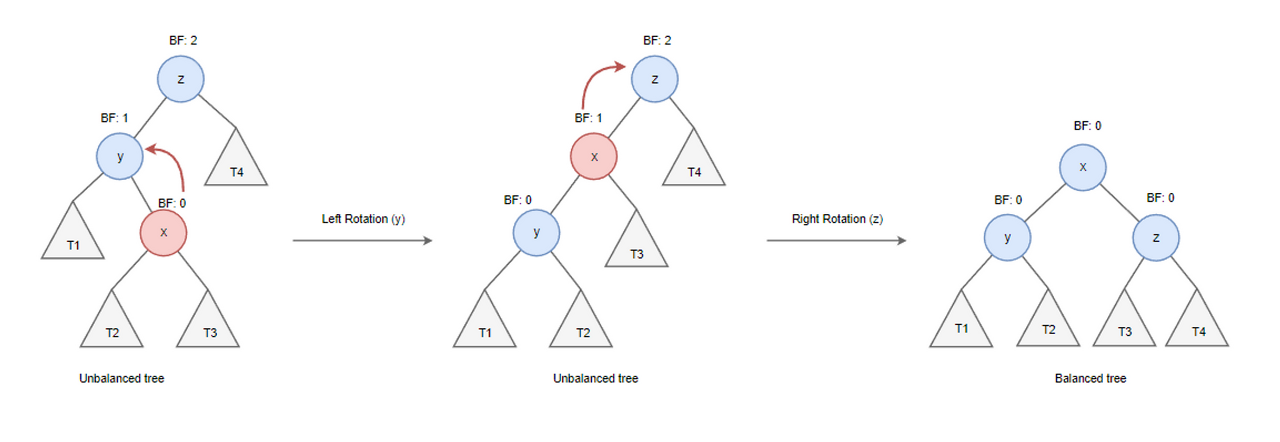
노드를 삭제할 때도 삽입과 마찬가지로 불균형이 발생하면 아래와 같은 순서로 회전을 통해 균형을 유지해야 합니다.
1. 해당 노드를 삭제합니다.
2. 노드를 삭제한 후, 삭제된 노드의 부모 노드를 시작으로 AVL 트리가 균형을 잃었는지 확인합니다.
3. 불균형이 발생한 경우, 발생한 불균형의 종류에 따라 회전을 수행합니다.
삭제된 노드의 자식 노드가 한 쪽에만 존재하는 경우, 해당 자식 노드를 삭제된 노드의 위치에 배치합니다. 이 경우에도 AVL 트리의 균형을 잃지 않도록 노드를 삭제한 후 rotation을 수행해야 할 수 있습니다.
AVL tree의 활용
AVL Tree는 다음과 같이 활용됩니다.
- 데이터베이스 시스템에서 쿼리 실행 계획을 생성하는 인덱스 구조를 작성할 때
- 자연어 처리 분야에서 문자열 검색 및 검색 결과의 정확도 개선이 필요할 때
- 게임 개발에서 오브젝트와의 충돌을 일관성있게 검사할 때
AVL 트리는 삽입과 삭제, 검색이 모두 O(logn)에 이루어지지만, 트리의 구현이 어렵고 균형 트리에 최적화된 B-tree가 존재하기에 상대적으로 덜 사용되고 있습니다.
- B-tree란?
[자료구조] B-tree란? / B-tree의 연산 / B*tree, B+tree
B-tree란? B-tree는 Self-balanced Tree 중 가장 유명한 자료구조입니다. Balanced-tree를 의미하며, 이진트리를 확장해 하나의 노드가 가질 수 있는 자식 노드의 최대 숫자가 2보다 큰 트리 구조입니다. 즉,
yeongjaekong.tistory.com
'CS > Data structure' 카테고리의 다른 글
| [자료구조] Red-Black tree란? / Red-Black tree의 원리 및 활용 (0) | 2023.05.29 |
|---|---|
| [자료구조] Splay tree란? / Splay tree의 원리 및 활용 (0) | 2023.05.25 |
| [자료구조] Graph란? / DFS와 BFS / 활용 및 예제 (백준 1260) (1) | 2023.03.21 |
| [자료구조] HashTable이란? / Chaining과 Open Addressing의 차이 / 예제 (백준 17219) (1) | 2023.03.13 |
| [자료구조] Heap과 Priority Queue란? / 활용 및 예제 (백준 11279) (0) | 2023.03.10 |
