Graph란?
그래프란 정점(Vertex)와 간선(Edge)을 모아놓은 자료구조입니다.
그래프는 사이클이 가능하고, 방향 그래프와 무방향 그래프가 모두 존재합니다.
이러한 점에서 그래프가 트리 구조의 상위 집합 개념이라 볼 수 있습니다.
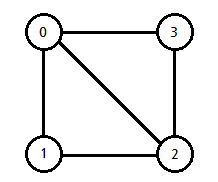
무방향 그래프에서 하나의 정점에 인접한 정점의 수를 차수(degree)라고 하며,
간선에 의해 직접 연결된 정점을 인접 정점(adjacent vertex)라고 합니다.
이러한 정점들을 지나는 경로가 같은 간선을 지나지 않을 때, 단순 경로(simple path)라고 합니다.(0 > 1 > 2 > 3)
그래프는 방향 그래프/무방향 그래프 외에도 간선에 가중치를 넣어 정점 이동 시 비용을 부과하는 가중치 그래프,
모든 정점에 경로가 존재하는 연결 그래프와 특정 정점에 경로가 존재하지 않는 비연결 그래프,
모든 정점이 연결되어 있으면서 트리의 속성을 만족하는 신장트리(Spanning Tree)와 신장트리의 가중치 합이 최소인 최소신장트리(MST) 등이 있습니다.
MST는 Greedy Algorithm인 kruskal Algorithm으로 구현할 수 있습니다.
Graph의 구현
그래프는 인접행렬과 인접리스트 두 방식으로 구현할 수 있습니다.
- 인접행렬
Vertex가 Edge로 직접 연결되어있으면 1, 그렇지 않으면 0인 2차원 배열을 통해 그래프를 구현합니다.
생성하는데 O(n^2)가 걸리지만, 생성한 후에는 O(1)의 속도로 탐색이 가능합니다.

- 인접리스트
리스트를 통해 Vertex와 연결되어 있는 노드를 해당 노드의 인덱스에 삽입하는 방식으로 그래프를 구현합니다.
탐색 시 O(n)의 속도가 걸리며, 인접행렬과 달리 필요한 공간만 사용하기 때문에 공간 낭비가 적습니다.
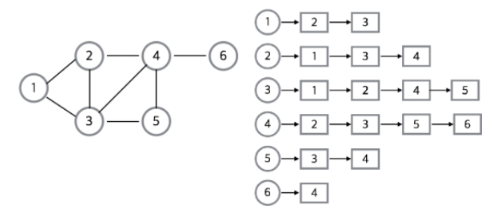
따라서 Vertex의 수에 비해 Edge의 수가 적은 Sparse Graph일 땐 공간 낭비가 적은 인접리스트를 사용하는게 좋고,
Vertex의 수에 비해 Edge의 수가 많은 Dense Graph일 경우엔 탐색이 용이한 인접행렬을 사용하는게 좋습니다.
DFS, BFS
DFS와 BFS 모두 연결된 그래프를 완전탐색할 때 사용하는 방법입니다.
- DFS란 Depth First Search, 즉 깊이 우선 탐색을 의미하며 한 노드에서 연결되어 있는 노드로 최대한 계속 나아가는 탐색 방법을 말합니다. 더이상 연결된 노드가 없을 때, 이전 노드로 돌아가서 다른 연결된 노드를 탐색하게 됩니다.
DFS의 경우 이전 노드로 되돌아갈 때 Last In First Out의 특성을 가진 Stack 혹은 재귀적인 특성을 이용하여 구현합니다.
저장 공간이 BFS에 비해 덜 필요하지만, 탐색 속도가 BFS보다 느리다는 단점이 있습니다.
- BFS는 Breadth First Search, 너비 우선 탐색을 의미합니다. 노드에서 가까운 노드를 먼저 방문한 뒤 그 다음 가까운 노드를 방문하는 탐색 방식입니다. DFS와 다르게 Queue를 통해 구현합니다.
탐색 속도가 빠르며, 큐에 다음 탐색할 정점들을 저장하는 방식으로 저장공간이 많이 필요하게 됩니다.
노드의 수가 많아질수록 탐색 시간이 커집니다.
따라서 각각의 경로마다 특징을 저장해야 하는 문제는 DFS, 가중치가 모두 같은 그래프에서 최단거리를 구해야 하는 문제는 BFS를 이용하는 것이 좋습니다.
Graph 예제
https://www.acmicpc.net/problem/1260
1260번: DFS와 BFS
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사
www.acmicpc.net
이 문제는 Input인 Vertex, Edge, root node의 Dfs, Bfs 결과를 각각 출력하는 문제입니다.
인접 행렬을 사용하여 구현하였습니다.
n, m, v = map(int, input().split())
matrix=[[0]*(n+1) for i in range(n+1)] #인접 행렬
visit = [0]*(n+1)
for i in range(m):
a,b=map(int, input().split())
matrix[a][b]=matrix[b][a]=1 #입력 간선을 연결
def dfs(v):
visit[v]=1
print(V, end=' ')
for i in range(1, n+1):
if(visit[i]==0 and matrix[v][i]==1):
dfs(i)
def bfs(v):
queue=[v]
visit[v]=0
while queue:
v=queue.pop(0)
print(v, end=' ')
for i in range(1, n+1):
if(visit[i]==1 and matrix[v][i]==1):
queue.append(i)
visit[i]=0
dfs(v)
print()
bfs(v)'CS > Data structure' 카테고리의 다른 글
| [자료구조] Splay tree란? / Splay tree의 원리 및 활용 (0) | 2023.05.25 |
|---|---|
| [자료구조] AVL tree란? / AVL tree의 연산 방법 및 활용 (0) | 2023.05.23 |
| [자료구조] HashTable이란? / Chaining과 Open Addressing의 차이 / 예제 (백준 17219) (1) | 2023.03.13 |
| [자료구조] Heap과 Priority Queue란? / 활용 및 예제 (백준 11279) (0) | 2023.03.10 |
| [자료구조] Tree란? / 활용 및 예제 (백준 1068) (0) | 2023.03.08 |
