[CV] Intensity Transformation / Filtering
Intensity Transformation
intensity(밝기)는 어떻게 구하나?
- RGB pixel 값으로 얻는 intensity 공식이 있음. ex) 0.2R + 0.7G + 0.1G, application에 따라 상세값은 달라짐
Contrast enhancement methods (대비 강화)
- mimax normalization : max-min, detail은 유지하나 contrast 변환이 제한적
- z-score normalization : 표준편차
- Histogram equalization : 픽셀 수의 누적으로 처리, detail 떨어짐
let L=2^bit count (e.g. 256)
minmax의 각 bit 계산 = (L-1) * ((Rk - Rmin) / (Rmax - Rmin))
histogram equal의 각 bit 계산 = (L-1) * the number of (sigma 0 to k) Rk / N * N, N은 픽셀 수.
Summary Questions
Q.
1. The intensity varies from 0 to 255 in 8-bit image, and it varies from 0 to ( ) in 16-bit image
2. How does the medical expert discriminate the intensity levels of 16-bit image?
3. If the image is black and white (binary), either (1 or ) will be stored at each pixel.
4. If the image is greyscale, it will store a ( ).
5. If it is a color image (RGB), it will store ( ).
6. Pros and Cons of each contrast enhancement method?
A.
1. 65535
2. window level
3. 1 or 0
4. range of intensities
5. sets of intensities
6. normalization의 경우 detail한 feature는 유지할 수 있지만 contrast 변화가 제한적이다.
max값이 outlier에 dependent하기에 outlier에 취약하다.
반면 histogram equalization의 경우 pixel별 intensity의 상대적인 세기에 대한 정보가 소실된다.
즉 detail은 사라지지만, outlier와 관계없이 contrast 변화시킬 수 있다.
Spatial Filtering
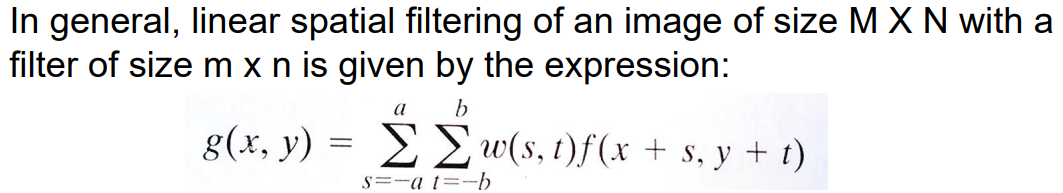
n by n Kernel이 2D image를 훑으며 filtering하는 방식. sigma (커널 픽셀의 위치와 이미지 픽셀의 곱)이며, 커널의 중앙값이 픽셀 값이 된다.
Correlation & Convolution
- Corr : 이미지를 필터로 이동시키면서 두 함수 곱의 합을 계산.
- Conv : 필터를 180도 회전시킨 후 Correlation 계산.
Smoothing - Purpose : noise reduction & 중요한 부분만 남기기 위함
※ 일반적으로 noise는 고주파다.
- Average(mean) filter : n*n 필터의 모든 값이 1/n^2. 따라서 스무딩 효과가 강하며, detail은 blur한다. 극단적인 cutoff로 인해 ringing과 같은 artifact가 생길 수 있다.
- Gaussian filter : sigma(= standard deviation)로 값의 범위(=필터링 정도)를 한정할 수 있다. sigma가 무한대일 때, average와 같은 효과.
- Median filter : 중앙값을 사용한다. salt and pepper(=impulse=speckle)과 같은 noise 제거에 탁월하며, average보다 detail을 잘 보존한다.
모든 mask(=kernel=window=filter)는 larger masks일수록 더 강한 스무딩 효과를 가진다.
Sharpening - Purpose : extract features
- Sobel filter : 1차 미분, 변화에 반응
- Laplacian filter : 2차 미분, 변화의 시작과 끝을 강조 - edge가 2중선이 되는 문제가 있음.
Summary Questions
Q.
1. There is ( ) between linear spatial filters and filters in the frequency domain
2. If the filter mask is ( ), correlation and convolution produce the same results
- Smoothing
3. Average filtering is a simple, intuitive and easy to implement method of ( ), i.e., reducing the amount of ( ) between one and the next. It is often used to reduce noise in an image
4. This process results in reduced sharp transitions. Because ( ) in intensity levels, the noise is reduced.
5. The median filter is normally used to reduce ( ) noise in images. It often does a better job than the average filter of preserving detail in the data, i.e., more selective/specific to the noise
6. The median is calculated by ( ) all the pixel intensities from the surrounding neighborhood into numerical order and next replacing the pixel intensity with the middle value.
7. Isolated clusters of pixels that are high or low with respect to their neighbors, and whose area is less than ( ) are eliminated by an MⅹM median filter
- Sharpening
8. The principal objective of sharpening is to ( )
9. Averaging is analogous to ( ), while sharpening is accomplished by ( ).
10. Image differentiation enhances edges and other ( ) even including ( ) and deemphasizes areas with slowly varying intensities
11. Masks of even sizes are awkward to implement because they do not have a ( ) with digital images
A.
1. one to one correspondence
2. 대칭
3. smoothing signals / variation
4. random noise typically consists of sharp transitions
5. speckle (impulse, or salt and pepper)
6. first sorting
7. M x M / 2
8. highlight transitions (extract features)
9. integration / differentiation
10. discontinuities / noise
11. center of symmetry
Filtering in Frequency domain
: spatial에서 복잡했던 filtering 연산을 FFT(Fast Fourier Transform) 등으로 간결하게 대체할 수 있음.
: 다른 방식의 filtering을 통해 spatial filtering으론 불가능하던 edge를 강조 및 noise 제거가 가능할 수 있음.
• Continuous IO, periodic, infinite : Fourier Series
• Continuous IO, aperiodic, finite : Fourier Transform
• Discrete IO, periodic, infinite : Discrete Fourier Series
• Discrete IO, aperiodic, finite : Discrete Fourier Transform
• Discrete input, Continuous output, aperiodic, infinite : Discrete Time Fourier Transform
※ Computer vision에서 주목할 것은 DFT다. 실제론 FFT를 쓰는데, DFT와 input과 output이 동일하나, 주기의 반복성을 활용해 DFT에서 efficiency를 수학적으로 높인 것이다.

* 2D DFT 예제) f(x,y) = [[1,2],[3,4]] 일 때 2D DFT의 결과는?

Low Pass Filter : 고주파 필터링 - edge, noise 등 filtering, blur처럼 보임. (smoothing과 유사)
- Ideal LPF : binary로 filtering
- Butterworth LPF : 지수함수(조절 o)로 filtering
- Gaussian LPF : 표준편차(조절 o)로 filtering
cutoff 강도 & ringing : ILPF > BLPF > GLPF
High Pass Filter : 저주파 필터링 - edge, noise 등 강조. (sharpening과 유사)
- Ideal HPF : binary로 filtering
- Butterworth HPF : 지수함수(조절 o)로 filtering
- Gaussian HPF : 표준편차(조절 o)로 filtering
Inherent Periodicity Problem - DFT와 IDFT는 주기성을 가지고 있기에 간섭으로 인해 2D 상에선 모서리가 둥그렇게 말리는 것처럼 보이는 wrap-around error가 발생한다. 이를 방지하기 위해 padding을 사용한다.
padding의 종류에는 zero padding, extension, mirroring 등이 있다. zero padding은 wrap-around error는 해결하지만 화면 상에 점처럼 생긴 artifact가 발생할 수 있다.
Summary Questions
Q.
1. Integration (summation) makes non-zero value, only when x(t) is multiplied with sinusoidal functions of the ( )
2. We can ( ) into various ( ) with different magnitudes and frequencies
3. In cases where tight control of the transition between low and high frequencies about the ( ) are needed, ILPF or BLPF presents a more suitable choice. The price of the control over the filter profile is the possibility of ( ).
4. This is important in such a medical imaging in which any type of ( ) is unacceptable.
5. DFT and IDFT has periodicity property. We must take into account the ( ) in the expression for the DFT
6. To obtain the correct result, ( ) must be used. Otherwise, we have a ( ).
7. If a 2D image size is M x N, the padded image size should be ( ) to avoid wrap-around errors of frequency filtering.
Padding is also necessary for spatial filtering to keep the image size from being reduced around boundary. If a 2D image size is M x N and a filter size is m x n, the necessary padded image size is ( ).
A.
1. 주기가 같을 때
2. decompose the signals / sinusoids
3. cutoff frequency / ringing
4. artifact
5. periodicity inherent
6. padding / wrap-around error
7. 2M x 2N (frequency의 주기성때문에 reflection) / M+m-1 x N+n-1