3DGS(SIGGRAPH 2023) 핵심 정리
Preview
https://arxiv.org/pdf/2308.04079
NeRF는 학습 시간이 매우 오래 걸린다는 단점이 있다.
당시 sota였던 Mip-NeRF가 학습에 48시간이 걸린 것에 비해, 3DGS 방법은 51분의 학습으로 Mip-NeRF보다 높은 성능을 보여줄 뿐아니라, 1080p 기준 30fps 정도의 실시간 렌더링까지 가능해져 엄청난 관심을 받게 되었다. 참고로 3DGS는 NeRF와 달리 MLP 방식을 사용하지 않는다. 3D Gaussian을 화면에 흩뿌려(Splatting) geometry의 정밀한 부분을 묘사하는, explicit representation 방법을 사용한다.
Method

SfM을 통해 pointcloud를 받아와서, 이 pointcloud 각각에 대해 가까운 세점과의 분산을 이용해 initialization해서 3D Gaussians을 얻는다. 이렇게 얻은 3D Gaussians에 색깔과 투명도를 입히고, 이를 입력 데이터셋에서 사용한 카메라 pose 방향으로 projection시켜 렌더링한다. 이후 g.t.와의 loss를 계산하고, 이 값을 바탕으로 3D Gaussian을 업데이트한다.
Keypoints
- Differentible 3D Gaussian
이 연구에서는 렌더링을 위해 3D Gaussian을 선택했다. 구에 가까워 미분 가능한 형태이기에, 원활한 학습이 가능하다.
3D Gaussian은 world space에서 정의된 전체 3D 공분산 행렬 에 의해 정의되며, 점(평균) 를 중심으로 한다. 이 Gaussian은 블렌딩 과정에서 로 곱해진다.
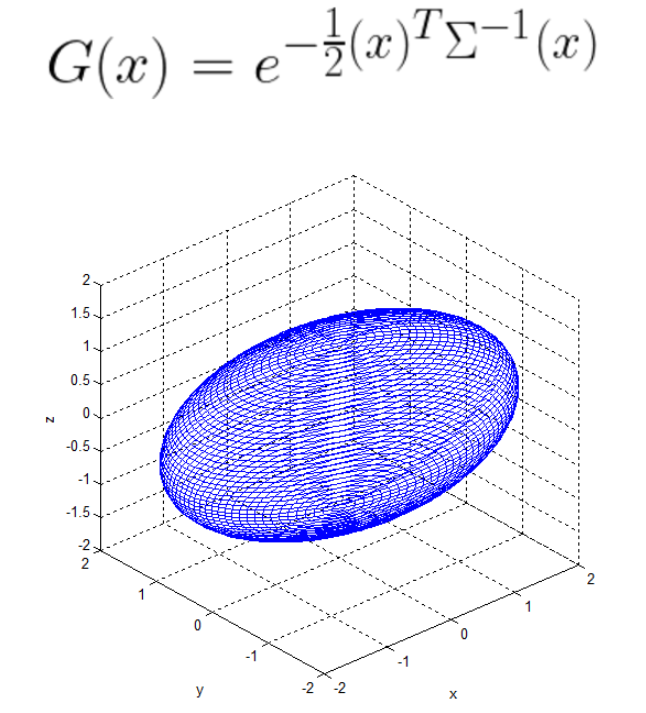
원래는 3D Gaussian을 2차원으로 투영하기 위한 Viewing transformation 가 주어지면 카메라 좌표의 공분산 행렬 은 비선형 변환을 아주 작은 공간에 대해 선형 변환으로 근사하는 Jacobian을 사용해야 한다.

하지만 이러한 방식은 gradient descent 시 여러 문제가 발생할 수 있다.
따라서 3D Gaussian의 공분산 행렬 타원체와 유사하다는 특징을 사용해, 복잡한 수학적 제약을 직접 다루는 대신 타원체의 형태를 조정하여 3D 공간에서 객체를 모델링하는 방식을 선택했다. 타원체의 크기와 방향은 스케일링 행렬 와 회전 행렬 로 정의되며, 이 두 행렬을 사용하여 해당하는 3x3의 공분산 행렬 을 찾을 수 있다.

- Adaptive Density Control

SfM에서 얻은 초기 sparse 점들로부터 장면을 더 잘 표현하기 위해 가우시안의 수와 밀도를 적응적으로 제어하는 방법을 사용한다. 위 그림을 보면, 재구성이 덜 된 영역에 있는 작은 가우시안의 경우 가우시안을 복제해 동일한 크기의 복사본을 생성하고, 위치 변화의 방향으로 이동시키는 것을 의미한다. 반면에, 큰 가우시안은 더 작은 가우시안으로 분할해야 한다. 이 과정에서 큰 가우시안을 두 개의 새로운 가우시안으로 대체하고, 스케일을 실험적으로 결정된 비율인 으로 나눈다. 또한, 새로운 가우시안의 위치를 초기화하기 위해 원본 3D 가우시안을 확률 밀도 함수(PDF)로 사용하여 샘플링한다.
100회 iteration마다 threshold() 이하의 투명도를 갖는 Gaussian을 제거하고, 3000회 iteration마다 Gaussian의 투명도를 0에 가깝게 설정해 학습 과정에서 투명도가 충분히 커지지 않은 가우시안을 컬링함으로써 가우시안 밀도의 불필요한 증가를 방지한다.
- Fast Differentiable Rasterization
rasterization이란 3D 공간상에 있는 물체를 2D에 매핑해서 표현하는 것이다. World Space를 화면 좌표로 변환 (3D -> 2D)할 때, 좌표계가 변해도 미분 가능해야하기 때문에 Viewing Transformation Matrix(W)와 Jacobian Matrix(J)를 사용해 선형 변환으로 근사한 형태로 공분산 행렬을 2x2 행렬로 변환한다.

3DGS는 고속 렌더링을 달성하기 위해 새로운 tile-based rasterizer를 사용한다. 병렬 처리를 위해 화면을 16x16개의 tile로 나눈 뒤, 스레드를 사용해 병렬적으로 타일별로 Gaussian을 컬링(제외)하며 동시에 결과를 공유한다. 컬링은 view frustum과 99% 신뢰 구간이 겹치는 Gaussians만 남긴다.
또한 전체 렌더링 과정에서 처리할 가우시안들을 깊이에 따라 정렬해 리스트에 넣어 각 타일에서 처리할 첫 번째와 마지막 가우시안을 식별하도록 했다. 가우시안을 누적하는 과정에서 픽셀의 투명도(α) 값이 설정해둔 임계점에 도달하면, 해당 스레드는 처리를 중단해 불필요한 계산을 줄이고 타일 내 모든 픽셀이 포화 상태에 도달하면, 해당 타일의 처리가 종료된다.

Loss는 L1 Loss(MAE)와 D-SSIM Loss에 가중치를 두어 사용했다. 논문에서

Q.
- Loss를 왜 저렇게 혼합해서 사용했는지에 대한 설명이 없다. 왜 저렇게 했을까?
그리고 ssim 기반의 loss를 사용한 것으로 보이는데, 뭔가 직관적으로 생각했을 때 성능 지표인 ssim, psnr, lpips로 loss를 잡으면 결과가 잘나올 것 같은데 실제론 안그럴까..?
=> 이미 그렇게 하는 경우가 종종 있다.
- output의 mip-nerf와 3dgs를 비교하면 학습시간은 매우 짧아졌지만 메모리 사용량은 매우 많아지는 tradeoff가 커보인다. 스레드를 통한 병렬 연산의 영향이 클 것 같은데, 그렇다면 이러한 아이디어를 NeRF와 같은 다른 프로세스에 적용하면 마찬가지로 메모리는 많이 쓰되 학습 시간을 개선할 여지가 있지 않을지? 실제로 그러한 연구가 진행되고 있는지?
=> 잘못된 생각. 메모리는 스레드 때문이 아니라, 3DGS는 Geometry를 저장하기 때문이다.